Programmatic Tiling in World Generation
A World of PG
Procedural generation (PG) is core to the roguelite experience. It enhances replayability by ensuring no two play-throughs are too similar, and pushes players to master essential game mechanics rather than relying on memorization of set pieces.
[Codename] Mad Mark will be no exception. Over the last weeks Carson and I have focused on building some foundational world PG so our gameplay can begin to incorporate some environmental variability and begin moving us in a rogue-y direction.
Standing up PG throughout our game world will bring along numerous technical challenges, crisscrossing many stages, layers of abstraction, and literal stacking of environmental elements. Here I'm sharing how we navigated one of our first PG implementation hurdles - automated "painting" of randomized patterns in the ground, and automated tile placement according to the resulting shapes in GameMaker: Studio 2.
The Result

My World is a Spreadsheet
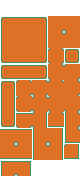
In this (poorly cropped) screen shot you can see the ground is composed of several different patterns. These patterns (the blotchy texture in the upper left and the dark blobs of dirt to the bottom and right) look as if they might have been carefully placed by hand. But this is not the case. They are random shapes formed from cleverly designed tiles that give the illusion of a natural and unique formation on the ground.
The process begins in a pretty abstract fashion. You can think of the environment as being divided into a grid (because it is). Each layer of tiles possesses its own grid to work with, and these grids are stacked on top of one another. Each of these grids starts out empty:
[0][0][0][0][0]
[0][0][0][0][0]
[0][0][0][0][0]
[0][0][0][0][0] ...etc
The patterns are brought into being by populating some cells and leaving the others blank. To create aesthetically pleasing figures however some care has to be taken into how the grid is populated. You can imagine that
[0][0][1][0][1]
[0][1][0][0][0]
[1][0][0][1][0]
[0][1][0][0][1]
Isn't going to look nearly as nice as
[0][0][0][1][0]
[0][0][1][1][1]
[0][1][1][1][0]
[1][1][1][0][0]
When filled out with tiles on our ground.
Enter Bob Ross
To encourage more pleasing shapes, we can't just iterate through the grid randomly assigning values of true and false. That would give us something more like the first example than the second. Instead, the shapes are 'painted' onto the grid by choosing a cell somewhere in the middle, and wandering in various directions at random with a 2x2 cell 'brush' that populates the true/false values.
(We use a 2x2 brush rather than a 1x1 because we found the results to be more pleasing. As a bonus, a 2x2 brush made many tile cases impossible, cutting the number of tiles we needed for a tileset from 47 to 23!)
In practice, the 'brushing' code looks like this in GMS2:
You can see we begin by picking an appropriate number of strokes to paint onto our grid, related in some arbitrary mathematical way to the grid's size (in this case based on a square root). Then, for each of those strokes the brush will move 1 to 4 times in one of the eight basic compass points. The result of some pretty natural looking smears that make nice dirt blobs once the tiles are laid down.
Figuring the Tiles
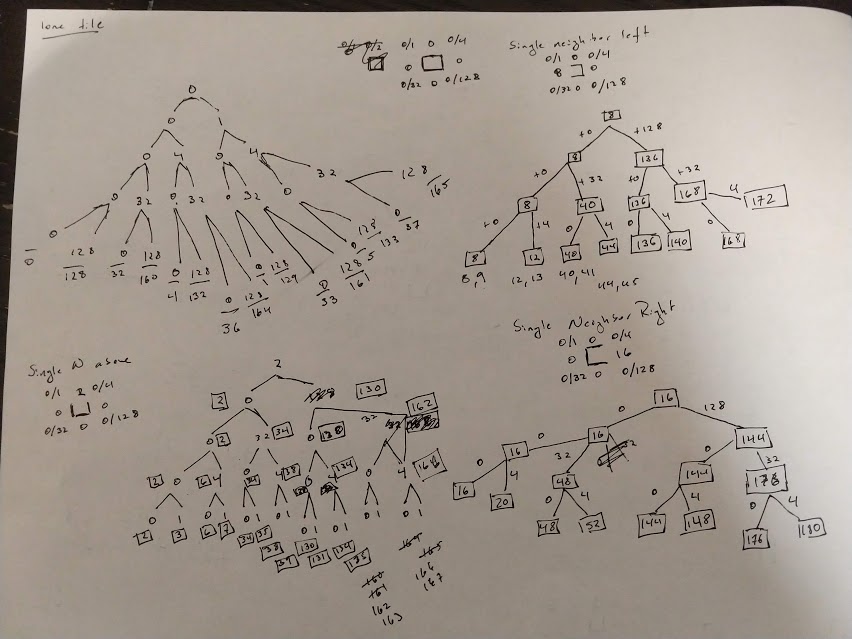
The next step is where the magic happens. That is, the actual laying down of the tile images into the game world. Selecting the correct tile image for a particular cell means looking at the arrangement of the neighboring cells to find the naturally fitting image. For example:
[0][0][0]
[0][1][0]
[0][0][0]
represents a single lone tile, which should have border edges on all sides. While
[0][0][0]
[1][1][0]
[1][1][0]
requires the 'upper right corner' tile image for a natural fit.
If single tile cells are allowed to be populated in your world without any neighbors, there will be 47 distinguishable arrangements requiring their own images. Any given cell (in the middle of the grid anyway) will have 8 surrounding neighbors, for 9 cells in all to establish a context. Because we only need to examine the populated cells to place tiles, we know the center tile in our 3x3 moving window will always be populated, and only the 8 surrounding cells can have variations. That means 2^8 = 256 distinct ways the 3x3 window can be populated, which reduce down to 47 when redundant cases are grouped together.
The challenge is to correctly map each area in the tile image to all 256 possible grid cell arrangements, and make this computation as efficient as possible (we'll be laying down a lot of tiles to create the world). In practice, this turned out to be more tedious than rigorously difficult. The arrangement of tile components in the tile image is more or less arbitrary, rather than being determined by any mathematical rules. So, the mapping from each grid cell case to individual images is also arbitrary in nature.
Mapping the arrangements of the 8 surrounding neighbor cells to a tile image means those 8 distinct values need to be reduced to a single key that can be used to perform a lookup, and that reduction needs to be done in a way that preserves uniqueness between the arrangements. This is done easily enough by assigning each neighbor cell either (a) a power of 2 value, or (b) zero. Like this:
[1] [2] [4]
[8] [0] [16]
[32][64][128]
So the upper right corner arrangement from earlier would become:
[0] [0] [0]
[8] [0] [0]
[32][64][0]
The cell values can then be summed, and in this case the number 104 tells us we need the upper right corner tile. No too hard to grasp, but figuring out which numbers represent which images is where the tedium comes in:
After about four hours of hand calculations I'd mapped each number from 0->255 to an image location (for the particular tile arrangement that Carson and I had settled on ). I decided to handle the actual implementation with a switch statement, though it could have been done numerous ways:
The '_tile_offset' value is an artifact of our tile arrangement lacking a spot for GMS2's alpha tile, and needing to be scooted down a cell row.
The result is reasonably snappy, taking about 400 milliseconds to place 16,000 tiles in a 6000x6000 room. In this case faster is always better, so I may return to see what I can do about latent speed ups if world tiling becomes a bottleneck. Maybe recycling the same piece of memory for the '_values' and '_surround' arrays (by hanging onto a ds_grid), or seeing if a hash table (in the form of a ds_map) works better than the hard-coded switch statement.
If you have any questions comment below. Happy tiling!
Files
Get Scoot Or Die
Scoot Or Die
Motorcycles with guns in the desert! A mini open-world rogue like
| Status | Prototype |
| Author | PerchDrunkThugz |
| Genre | Adventure, Survival |
| Tags | Driving, Open World, Pixel Art, Roguelike, Tactical |
More posts
- Version 0.2.0 UpdateDec 18, 2019
Leave a comment
Log in with itch.io to leave a comment.